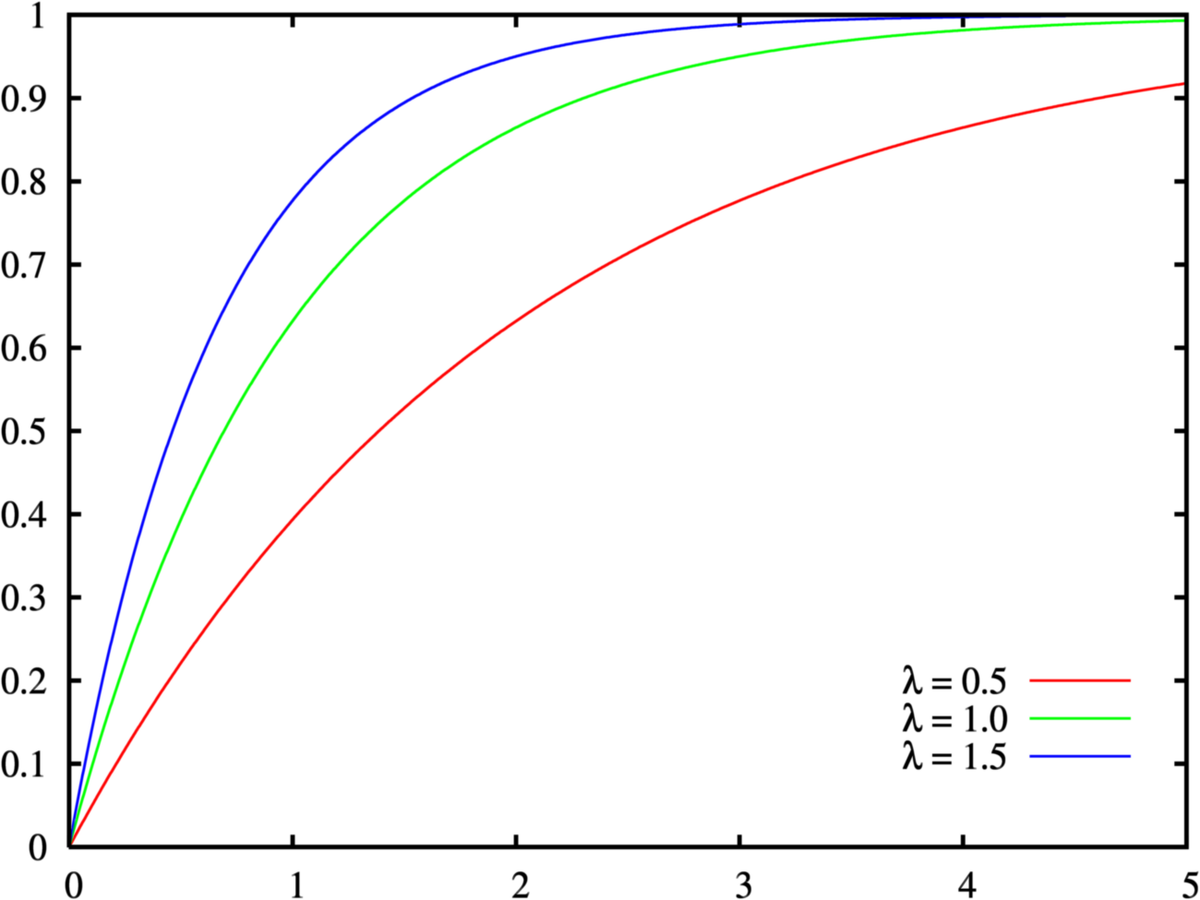
 Cumulative distribution function for the exponential distribution Cumulative distribution function for the normal distribution In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable , or just distribution function of , evaluated at , is the probability that will take a value less than or equal to . [1] Every probability distribution ...
Cumulative distribution function for the exponential distribution Cumulative distribution function for the normal distribution In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable , or just distribution function of , evaluated at , is the probability that will take a value less than or equal to . [1] Every probability distribution ...