 The probability of drawing any set of green and red marbles (the hypergeometric distribution) depends only on the numbers of green and red marbles, not on the order in which they appear; i.e., it is an exchangeable distribution.
The probability of drawing any set of green and red marbles (the hypergeometric distribution) depends only on the numbers of green and red marbles, not on the order in which they appear; i.e., it is an exchangeable distribution.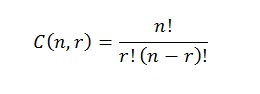 The hypergeometric distribution is a discrete probability distribution that calculates the probability an event happens k times in n trials when sampling from a small population without replacement.
The hypergeometric distribution is a discrete probability distribution that calculates the probability an event happens k times in n trials when sampling from a small population without replacement.